Masking-friendly signatures and the design of Raccoon

By _PQShield Blog

December 11, 2023

In this blog post, I will discuss the class of attacks known as side-channel attacks (SCA), how masking is an effective countermeasure against SCA, why masking Dilithium is difficult and how we designed our masking-friendly scheme Raccoon!

In 2022, NIST unveiled the first schemes selected to be NIST PQC standards: Kyber for key encapsulation, and Dilithium, Falcon, and SPHINCS+ for digital signatures. The security of these schemes has been extensively studied, and we are confident in their mathematical foundations (lattices and hash functions). However, when deploying them one should pay special attention to side-channel attacks.

Side-channel attacks (SCA)

When a physical device executes an algorithm, it may physically leak information about the type of operation, or the data being processed. For example, a computationally expensive operation may drain the battery of your smartphone or heat it up. This leakage may manifest via other forms, such as the running time, electromagnetic emissions, or acoustic emission of the device. Sometimes, even the distant flickering of a LED can be exploited (Ars Technica). The umbrella term side-channel attacks (SCA) encompasses all attacks that leverage such leakage to compromise sensitive data. This toy example from a research paper (ACM) displays the electric potential of a laptop using an RSA private key to decrypt a message. The bits of the private key (in red) are clearly correlated to the signal being measured (in blue).

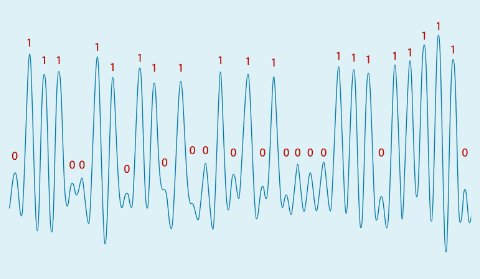
Post-quantum schemes are no less vulnerable to SCA than their classical counterparts. For example, several SCA have been demonstrated against Dilithium (PQCrypto, TCHES). In contexts where SCA can be mounted, adequate countermeasures need to be in place.

Defeating SCA with masking

There exist many ways to mitigate SCA. I will focus on masking, since it is the most studied countermeasure, as well as one of the most generic, most effective and most common. Masking consists of splitting each sensitive variable into d random shares, such that adding all shares recovers the variable. For example, consider x = 9 in the modular ring ℤ16 = ℤ / 16ℤ. A valid masking of x with 3 shares would be (12, 5, 8), since (12 + 5 + 8) mod 16 = 25 mod 16 = 9.

The idea behind masking is that sensitive data is distributed across several shares, making it harder for an attacker to simultaneously learn the values of all shares. Experiments and analyses show that when masking with d shares, the cost of an attack increases exponentially in d. This gives us a reason to set d as high as possible.

The hard part, however, is that we need to be able to perform useful operations on masked data. Some operations are easy to perform. Addition modulo q is one of them: (12, 5, 8) is a valid sharing of 9, (7, 2, 10) is a valid sharing of 3, and one can see that (12 + 7, 5 + 2, 8 + 10) = (3, 7, 2) is a valid sharing of 9 + 3 = 12. Note that this only requires d additions in the ring ℤ16, so masked addition is an efficient operations. More generally, linear operations (including multiplying a masked vector by a matrix) are easy to mask efficiently. However, not all operations are easy to mask.

To read the full article, click here