IP Catalog > Elliptic

Elliptic IP

Filter
Filter

Login required.

Sign in

Login required.

Sign in

Login required.

Sign in

Search (43)
Compare 43 IP from 16 vendors (1 - 10)
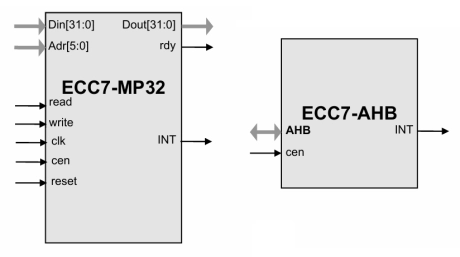
  • ECC7 Elliptic Curve Processor for Prime NIST Curves
    • Elliptic Curve Cryptography (ECC) is a public-key cryptographic technology that uses the mathematics of so called “elliptic curves” and it is a part of the “Suite B” of cryptographic algorithms approved by the NSA.
    • The design is fully synchronous, with the exception of the seed part, and available in both source and netlist form.
    • The core is supplied as portable Verilog (VHDL version available) thus allowing customers to carry out an internal code review to ensure its security.
    Block Diagram -- ECC7 Elliptic Curve Processor for Prime NIST Curves
  • Elliptic Curve Digital Signature Algorithm
    • Supported Elliptic Curves
    • other/custom curves optional support
    • Optional Side Channel Attacks countermeasures
    • Input/Output EC point verification
    • Fully synthesizable, synchronous design
  • Elliptic Curve Digital Signature Algorithm
    • Basis The ECDSA functions of CryptOne are powered by a collection of reliable and efficient algorithms and protocols. These techniques quickly and accurately generate and verify digital signatures using the fast execution of elliptic curve-based mathematical operations.
    • CryptOne's ECADSA implementation satisfies strict security criteria by conforming to the FIPS 186 standard, guaranteeing compatibility and interoperability with a broad range of cryptography solutions.
  • Elliptic Curve Cryptography IP
    • Supported algorithms:
    • Point multiplication
    • ECDSA signature generation
    • ECDSA signature verification
  • High-Speed Elliptic Curve Cryptography Accelerator for ECDH and ECDSA
    • Fully digital design
    • Portable to any ASIC or FPGA technology
    • Fully standard compliant
    • Easy to integrate
    Block Diagram -- High-Speed Elliptic Curve Cryptography Accelerator for ECDH and ECDSA
  • high-performance solution for elliptic curve cryptography
    • Supported algorithms:
    • Supported Elliptic Curves
    • Optional Side Channel Attacks countermeasures
    • Input/Output EC point verification
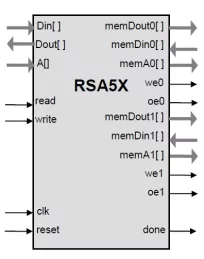
  • Scalable RSA and Elliptic Curve Accelerator
    • The core implements the exponentiation operation of the RSA cryptography Q = Pk.
    • The operands for the exponentiation: k and P as well as the modulus are programmed into the memory and the calculation is started.
    • Once the operation is complete, the result Q can be read through the interface.
    Block Diagram -- Scalable RSA and Elliptic Curve Accelerator
  • Elliptic Curve Digital Signature generation and verification
    • Supports any EC over GF(p) of the simplified Weierstrass form that is commonly defined in ECC standards such as NIST, SEC2, Brainpool
  • Elliptic Curve Point Multiply and Verify Core
    • ECC1 implementation is unencumbered by any patents
    • Small size: ECC1 requires less than 10K ASIC gates
    • High throughput for long life battery powered applications: 5,000 point multiplications per second in the 65 nm ASIC process
    • Support for the NIST ECC binary fields 2163, 2233, 2283, 2409, and 2571
  • Crypto Box Toolset Secure Accelerator
    • The High-Performance Hybrid Crypto Box IP core delivers maximum cryptographic throughput by combining classical asymmetric (RSA, ECC), symmetric (AES), and hashing (SHA-2/HMAC) engines with a dedicated post-quantum accelerator supporting ML-KEM (Kyber) and ML-DSA (Dilithium).
    • Designed for performance-critical systems without tight area or power limitations, this IP enables ultra-fast key exchange, digital signatures, and secure data processing.
×
Semiconductor IP