Elliptic IP
Filter
Compare
46
IP
from
17
vendors
(1
-
10)
-
ECDSA (Elliptic Curve Digital Signature) IP Core
- Full ECDSA implementation adhering to Standards for Efficient Cryptography (SEC)
- Bitcoin algorithm support
- Technology-independent HDL model
- Simple external interface for easy adaptation
-
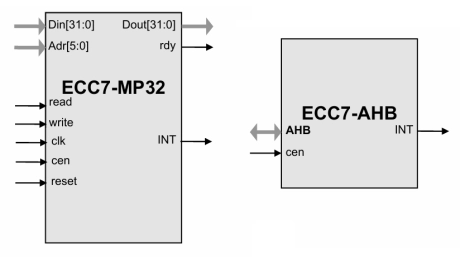
ECC7 Elliptic Curve Processor for Prime NIST Curves
- Elliptic Curve Cryptography (ECC) is a public-key cryptographic technology that uses the mathematics of so called “elliptic curves” and it is a part of the “Suite B” of cryptographic algorithms approved by the NSA.
- The design is fully synchronous, with the exception of the seed part, and available in both source and netlist form.
- The core is supplied as portable Verilog (VHDL version available) thus allowing customers to carry out an internal code review to ensure its security.
-
Elliptic Curve Digital Signature Algorithm
- Supported Elliptic Curves
- other/custom curves optional support
- Optional Side Channel Attacks countermeasures
- Input/Output EC point verification
- Fully synthesizable, synchronous design
-
Elliptic Curve Digital Signature Algorithm
- Basis The ECDSA functions of CryptOne are powered by a collection of reliable and efficient algorithms and protocols. These techniques quickly and accurately generate and verify digital signatures using the fast execution of elliptic curve-based mathematical operations.
- CryptOne's ECADSA implementation satisfies strict security criteria by conforming to the FIPS 186 standard, guaranteeing compatibility and interoperability with a broad range of cryptography solutions.
-
Elliptic Curve Cryptography IP
- Supported algorithms:
- Point multiplication
- ECDSA signature generation
- ECDSA signature verification
-
High-Speed Elliptic Curve Cryptography Accelerator for ECDH and ECDSA
- Fully digital design
- Portable to any ASIC or FPGA technology
- Fully standard compliant
- Easy to integrate
-
high-performance solution for elliptic curve cryptography
- Supported algorithms:
- Supported Elliptic Curves
- Optional Side Channel Attacks countermeasures
- Input/Output EC point verification
-
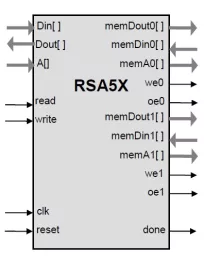
Scalable RSA and Elliptic Curve Accelerator
- The core implements the exponentiation operation of the RSA cryptography Q = Pk.
- The operands for the exponentiation: k and P as well as the modulus are programmed into the memory and the calculation is started.
- Once the operation is complete, the result Q can be read through the interface.
-
Elliptic Curve Digital Signature generation and verification
- Supports any EC over GF(p) of the simplified Weierstrass form that is commonly defined in ECC standards such as NIST, SEC2, Brainpool
-
Elliptic Curve Point Multiply and Verify Core
- ECC1 implementation is unencumbered by any patents
- Small size: ECC1 requires less than 10K ASIC gates
- High throughput for long life battery powered applications: 5,000 point multiplications per second in the 65 nm ASIC process
- Support for the NIST ECC binary fields 2163, 2233, 2283, 2409, and 2571